¿Cómo se ordenan los datos en un cubo OLAP de EPM?

Quiero tomarme unos momentos para compartir con una labor "evangelizadora" respecto a los cubos multidimensionales que usamos en EPM (Enterprise Performance Management).

En ocasiones, cuando hablo con compañeros acostumbrados a trabajar con bases de datos relacionales, observo que no ordenamos las cosas en nuestra cabeza del mismo modo que cuando hablamos de datos o de registros.

Lo que os quiero compartir es una idea que creo que es bastante universal en el mundo EPM y que es la base de cómo encontrar cosas dentro de un cubo OLAP, especialmente en aquellos casos en los que la información se almacena en un sistema propietario y no en una base de datos relacional al uso, que podamos explotar con herramientas de terceros (como SQL Server u Oracle SQL Developer). 

¿Os acordáis en el cole cuando nos enseñaban los números complejos?

Un número complejo es aquel que consta de una parte real más una parte imaginaria:

a+bi

Y recordaréis que esto no es más que otro modo de representar un par de números en un eje de coordenadas:

(a,b)

Esas coordenadas nos permiten "pintar" un punto en un plano cartesiano, así como un vector que une el origen con el punto en cuestión. De ese modo, podemos decir que a y b son las componentes del vector, son sus coordenadas, que nos indican dónde hallar ese punto.

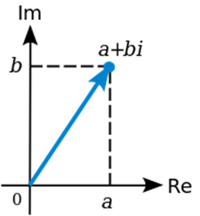
Además, podemos calcular un valor para ese punto, o lo que también se conoce como el "módulo" del vector, el cual se calcula mediante el Teorema de Pitágoras, donde si a y b son los catetos de un triángulo recto, podemos calcular la hipotenusa (que no es otra cosa que la longitud o módulo del vector en cuestión) como:

Así que, para unas coordenadas dadas, podemos obtener un valor numérico. Esta es la idea a la que quería llegar, porque,

¿Qué tiene que ver esto con el cubo OLAP o los cubos multidimensionales en EPM y la manera de ordenar información en ellos?

Desde el punto de vista matemático, tiene que ver muy poco. Pero desde el punto de vista funcional, mucho.

La idea es que las componentes (coordenadas) de un vector nos permiten hallar un dato.

Un ejemplo de la vida real:

Esto constituye la base de cómo se ordena la información (los hechos) en una base de datos multidimensional, y es lo que algunos llamamos un "vector de datos".

En un cubo base de datos multidimensional de EPM, más que hablar de "registros", es apropiado hablar de "vectores de datos", donde las componentes de cada dimensión nos van a decir dónde encontrar un valor (un hecho).

Por ejemplo:

Si en el mes de junio 2020 se han gastado 200000 € en sueldos y salarios, esto en una base multidimensional podría representarse como:

(Jun, 2020, Real, €, Sueldos y Salarios) = 200000

Esto correspondería a un vector de datos de un cubo de 5 dimensiones con la siguiente morfología:

(Periodo, Año, Escenario, Moneda, Cuenta) = *#hecho*

Espero que os haya sido útil esta explicación, que pretende acercaros a un modo de comprender cómo se ordenan los datos en un cubo OLAP de EPM.

Pincha aquí para encontrar más artículos sobre EPM